～数学的思考　命題で考える～

 

 

私というか甲野家は代々理数系の家系で父親、姉、祖父、曾祖父が理数系の勉強をしてきました。私も中学校まで学校の成績が良い方ではなかったのですが数学は割と得意でした。小学校低学年の頃からユニット折り紙を作ってきたので図形が得意でした。地元公立の小中学校を卒業したあとは私立の高校に進学し、２年生から理系コースへ。そこで物理学が好きで得意となり、東京理科大学応用物理科進学に至ります。物理を学ぶには数学が必須で物理数学という分野があるほど。物理は別格として、数学は大いに勉強し苦しめられた科目です。

 

私の大学受験当時言われたことですが、数学は国語ができないといけない、という考えがあります。一見離れているように見える国語と数学。しかし理数系学科への大学受験の数学を乗り越えるためには国語の文章読解能力が必須なのです。大学受験レベルでは、〇＋△を答えよ、みたいな数式を解かせるような問題は少なく数式自体を導き出す必要があるものばかり（※当時のセンター試験、現在の共通テストではそのような問題があるかもしれませんが。）。問題文の文章を理解しなければ先に進めないのです。

また前提条件を見落とすと誤答に繋がるので注意深くする必要があります。よくある話ですが、１＋１＝？という問題で、普通ならば２と答えを出すでしょうが、これが２進法だとすると答えは１０。どこにも１０進法とは書いていないのだから、どういう条件ですか？と疑問に持つのが数学をしてきた人の心理。そのため物事を理解する際に疑い深く細かくなる傾向があります。

 

大学までの授業で数学的思考を身につけたことは社会人になってから非常に役立っています。どのように役立っているのか具体的にいうと“命題”というものを知っていることが一つの例。

 

数学において命題（proposition）とは、真偽の判断の対象となる文章または式・定理または問題のことを言います。これだと分かりにくいのでもう少し表現をすると『正しいか正しくないかが明確に決まる文や式』のことを命題といいます。例えば『私は鍼灸師である』という文章。これはチェックすれば（鍼灸師免許があるかどうかを確認すれば）真偽が分かるので、命題と言えるのです。

 

数学では、『p ならば q』という命題を、『p⇒q』と数式で表現します。ここでのp は『仮定』、q が『結論』、⇒は『“ならば”という条件』という意味になります。これを踏まえて用語の定義と説明を加えます。『仮定』pに対して“pではない仮定”を『pの否定』として⁻pとします（※本来の表記はｐの上に横棒をおく）。同じように『結論』qに対してを“qでいない結論”を『qの否定』⁻qといいます。

 

代数（アルファベットで表す任意の項目）で書くと分かりづらいので例題としての命題を挙げましょう。「東京都民は日本人である」。これを命題とします。この場合『仮定』pが「東京都民であるならば」、『結論』qが「日本人である」、『仮定の否定』⁻pが「東京都民でないならば」、『結論の否定』⁻qが「日本人ではない」となります。まとめると以下の通り。

 

『命題』p⇒q：「東京都民は日本人である」

『仮定』p：東京都民であるならば

『結論』q：日本人である

『仮定の否定』⁻p：東京都民でないならば

『結論の否定』⁻q：日本人ではない

 

このように考えると文章を読んだときに、それはp（仮定）なのかq（結論）なのかを読み取るくせができます。そしてそれらを否定する⁻pや⁻qは何になるのか、を考えるようになります。ここから更に用語の定義を増やします。

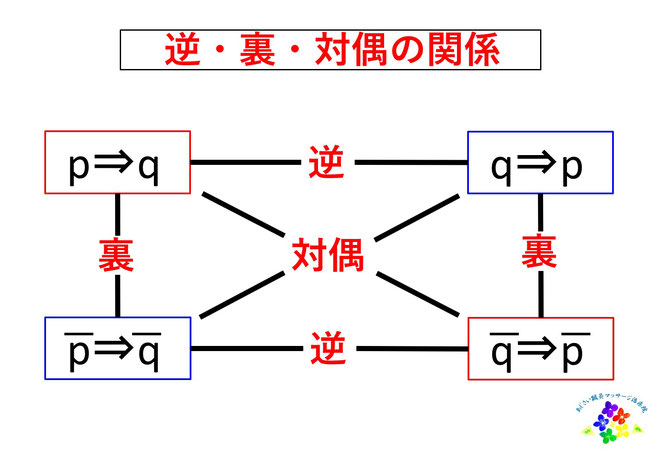
『命題』「p⇒q」（pならばq）において、「q⇒p」 （qならばp）を『逆』、「⁻p⇒⁻q」（pでないならばqではない）を『裏』、「⁻q⇒⁻p」（qではないならばpではない）を『対偶』といいます。ここまで書くと面倒くさくてよく分からないと思います。最初の『命題』「東京都民は日本人である」で当てはめてみましょう。

 

『命題』p⇒q（pならばq）：「東京都民は日本人である」

『逆』q⇒p（qならばp）：「日本人ならば東京都民である」

『裏』⁻p⇒⁻q（pでないならばqではない）：「東京都民でないならば日本人でもない」

『対偶』⁻q⇒⁻p（qではないならばpではない）：「日本人でないならば東京都民ではない」

このようになります。

 

『逆』はそのまま仮定と結論の順番が入れ替わって逆になっています。

『裏』は否定の仮定に否定の結論で、命題と順番は同じです。

『対偶』は仮定と結論の順番が入れ替わっていて、かつ仮定・結論どちらも否定となっています。

 

どうでしょうか。数式で表現されていますが国語、文章読解力の話になりませんか。このようなことを数学では学びます。ではこれらが何の意味があるのでしょうか。更に証明というものを持ち出します。

数学において証明（Mathematical proof）とは、ある命題が正しいことを主張するための一連の演繹のこと、としています。つまり命題p⇒qが正しいのかそうでないのか（真偽）を確かめることです。その証明が数学では非常に厳密で立証するのが難しいのです。例えば直角三角形において長辺の二乗と短辺の二乗を足した数値は斜辺の二乗に等しいというピタゴラスの定理があります。これはどのような形の直角三角形においても適応されるのですが、それを証明することは簡単ではないことがお分かりになるでしょうか。辺の長さが無限にあり、どの形・大きさでもピタゴラスの定理は成り立つことを実証する方法。数学において“証明する”という行為は簡単なことではなく、数学を学んでいる人ほど簡単に「証明されました！」とは言わないのです。それも数学をしている人は細かい、面倒くさいと言われる所以です。

 

細かいことは省きますが、命題の真偽と命題の対遇の真偽は一致します。どうしてかは大変なので説明しません。とにかく命題が正しいとしたらその対偶も正しく、命題が間違っているとしたらその対偶も間違っているのです。命題を証明するために対偶の真偽を検証する証明方法があります。例えば命題として「はり師は東洋医学を勉強している」を証明しようとしてみましょう。

 

『逆』「東洋医学を勉強している者ははり師である」 。

『裏』「はり師でなければ東洋医学を勉強していない」。

『対偶』「東洋医学を勉強していないならはり師ではない」。

この対偶を考慮すると、東洋医学を勉強していない人間がはり師であることはまず考えられないので、『対偶』は正しいだろう。よって命題「はり師は東洋医学を勉強している」は正しいということになる。というわけです。

 

しかし、文章の内容を厳密にみていかないと意味がありません。

まず“はり師”とは“はり師国家試験に合格して名簿登録されていてはり師免許を取得している者”である前提があります。この前提は日本の法律上のことで、海外では条件が変わる可能性があります。続いて“東洋医学を勉強している”というのはどのレベルで勉強しているということでしょう。曖昧なのです。ブログ、サイトを目にした。一般向けの東洋医学を紹介する本を読んだ。カルチャースクールで習ったことがある。はり師国家試験合格レベルの勉強をしている。はり師国家試験に合格している。どの程度を“東洋医学を勉強している”というのでしょうか。この『命題』（p⇒q）を証明する以前に、『仮定』（p）と『結論』（q）を明確に定義しないと証明しようがないわけです。

 

このように数学の命題を利用して物事を捉えると、問題を正確に把握する訓練になるのです。

 

甲野　功

 

電話　　　：070-6529-3668

メール　　：kouno.teate@gmail.com

ＬＩＮＥ　：@qee9465q

 

ご連絡お待ちしております。

 

院長の書いたコラムブログはこちら→詳しくはこちらへ