～数学的思考　微分積分で物事を考える～

三角関数（サイン、コサイン、タンジェント・・・）と並び、それは社会で使うことあるの？と言われるのが微分積分ではないでしょうか。三角関数も微分積分も数学で学ぶ内容。義務教育の範囲内だと思います。高校２年生から理科系コースを選び、東京理科大学応用物理科を卒業したので知っていて当たり前というか非常に身近にあったこの２つ。最近視聴した池上彰さんの経済番組で、「微分積分は何の役に立つのですか？」とゲストのタレントが質問していました。それが世間の意見ということでしょう。

微分積分について今でも忘れられないエピソードがあります。高校時代に数学の授業で

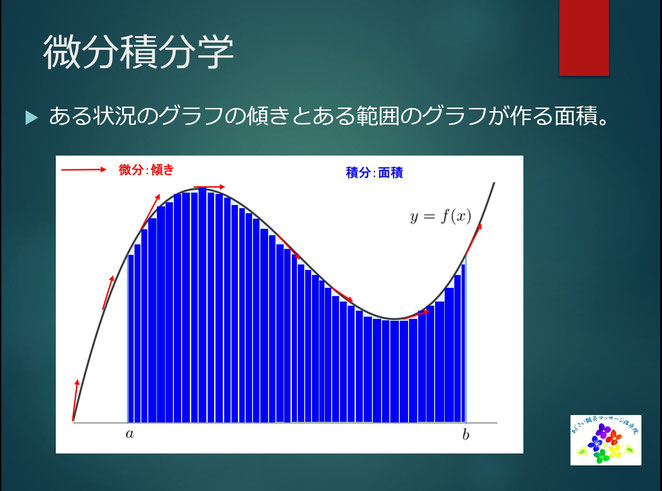
＜微分はそのときの勢い、積分は実績＞

ということを習いました。経営的なことで考えるとイメージがつくということです。

日々の売上をプロットしていき折れ線グラフにしたとします。グラフの傾きが微分であり、そのときの勢いを表します。大きく上向いているのか、平坦なのか、下降しているのか。その時点での経営の勢い（上昇も下降も含めて）を微分によって確認できる。そしてある範囲においてグラフと横線（時間軸）を垂線で囲んだ面積が積分であり、それが実績であるということ。例えば売上の低空飛行が続いていても長い期間でみるとその囲まれた面積は広くなり、それが実績である。急激に売上が上昇しても（傾きが正の方向に大きい）グラフが消えてしまったらその範囲の面積は思ったよりも広くなりません。積分は一定期間の状態をみることで残してきた実績を測ることでるというわけです。

微分積分が社会でどのように活用されているのかを教えてもらいました。複雑な数式を解くことが数学の授業ですが、社会の必要に迫られてそれがあることを学ぶ。この話は３０年くらい前のことですが記憶に残っていて、経済・経営には数学は必要だという事を心に刻んだものでして。このときの数学の先生は当時の担任であり、部活の顧問でありました。

このことを昨年、鍼灸マッサージ専門学校の学生さんに話をしたことがあります。参加者はまさに、「数学って我々の仕事に関係あります？」という感じでした。そのときに微分積分はどのようなもので、社会に活用されているのだよと説明したのです。

微分積分は学問として微分積分学（calculus）であり、解析学の基本的な部分を形成する分野の一つとなります。それは局所的な（瞬間的な）変化を捉える『微分』と、大局的な集積を扱う『積分』の二本柱からなります。字でみると『微分』は細かく（“微”細に）“分”けることで、それらを“積”み“重”ねるのが『積分』といえます。先に例を挙げたように、微分はその瞬間でどれくらい変化をしているのかをみているもので、グラフの傾きに相当します。積分はどれくらい積み重ねたのかをみているもので、グラフで囲まれる面積に相当します。

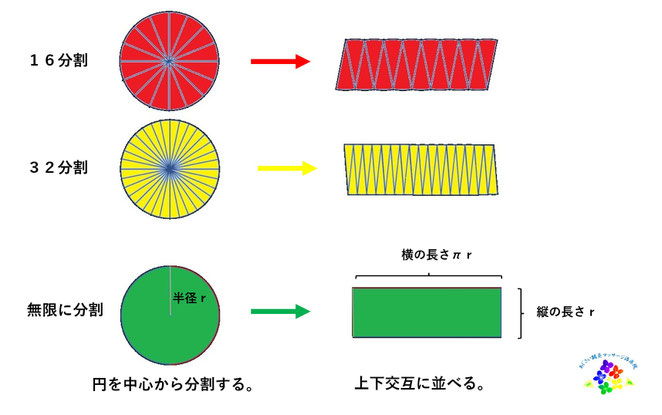
私達が最初に習う微分積分は「円の面積」でしょう。四角形の面積は縦かける横で計算できます。では円の面積はどうしたらよいでしょうか。円をピザを切るように中心から均等に分けていきます（これが微分）。それらを上下交互に並べていきます（積分）。無限に分けていって並べるとその形は長方形にどんどん近づいていきます。そのとき縦が半径（ｒ）、横が円周の半分（πｒ）。よって掛け算するとπｒ²となり、これが円の面積となります。

※説明

円周率π：直径と円周の比率。もしも直径が１ｃｍだとしたら円の周囲（円周）は３．１４１５ｃｍになります。πは無理数なので無限に小数点以下の数字が続きます。約３あるいは３．１４とされます。

半径ｒ：直径の半分。コンパスで円を描くときに開く幅。

円周は２πｒで表される（πは定数、ｒは任意の数）。面積を求めるときは分けた辺を並べたときに横の長さが上下合わせて円周になるため２分の１でπｒになる。十分に分けて上下交互に並べたらほぼ長方形とみなしてその面積はｒ（縦）×πｒ（横）、すなわちπｒ²となるのです。

このことを応用すると一見歪な形、曲線で囲まれたものでも面積を計測することができます。応用すれば体積でも。単位当たりのブロックを作り、それを数える。それが微分積分の基本になります。

この微分積分を発見したと言われているのが有名な物理学者アイザック・ニュートンです。リンゴが樹から落ちた様子をみて万有引力を発見したという逸話で有名ですね（本当な作り話という説もありますが）。ニュートンは「近代物理学の創設者」であり「微分積分の発見者」と称されます。微分積分学の基本定理を発見し、それまで別の学問であると思われた微分法と積分法を統一したのでした。余談ですが、私が中学生の頃読んだ科学者の伝記マンガに登場したガリレオ・ガリレイ、アイザック・ニュートン、アルバート・アインシュタインの３名から大きな影響を受けて後に大学で物理学を学ぼうと思わせたのです。

移動距離を時間で微分すると速度に、速度を更に時間で微分すると加速度になります。反対に加速度を積分すると速度に、速度を積分すると移動距離になります。微分と積分は相対するものになります。

※説明

ｘ：移動距離

ｖ：速度

ａ：加速度（どれくらい速度が変化したのか）

ｔ：時間

ｖ₀：初速度（最初の速度）

数式にすると、速度ｖ＝ｖ₀＋ａｔ。これを時間ｔで微分する（ｄｖ/ｄｔ）と、加速度がａ（＝ｄｖ/ｄｔ）。速度ｖを時間で積分する（∫ｖｄｔ）と移動距離ｘ＝１/２ｖ₀ｔ＋ａｔ²になる。移動距離ｘを時間で微分する（ｄｘ/ｄｔ）と速度ｖになる。

他にも運動量保存則を積分するとエネルギー保存則になるのです（説明は省きます）。このように物理学から数学の微分積分が生まれといえます。物理学を学ぶには数学が必須であるので私にとって数学は近い、というか利用しなければいけないもの、という印象です。

物理学を勉強することや円の面積を出すときに微分積分が使われますが、経営の数字を見るときに考え方を知っているだけでも有利になります。私が一番その著書を買ってきたのが森岡毅氏なのですが、氏は数学を用いて経営再建や新規事業を行う数学の実践者です。微分積分なんて実社会に役に立たない、という意見は偏見だと思っていて、むしろとても身近な数学ジャンルの一つだと捉えています。

それを表すのが「ロングテール戦略」ではないでしょうか。これは物流の王者Amazonが行った有名な経営戦略です。多品種の商品を扱う場合、どれもが均等に売れるという事はなく、売れ筋とあまり売れないものに分かれます。それを売上順に並べると反比例グラフのような形になります。前の方に高い売上商品が並び、どんどん背が低くなる。ある程度いくと低い売上製品が延々と並んでいきます。この形はどの業界でも大体同じようになるのです。従来店舗では物理的に店頭に並べる商品数に限界があるため、売れ筋商品に絞って店頭販売します。狭小店舗であればよりシビアになりますし、大型店舗でも商品数は有限です。しかしこの販売方法はどこも同じような商品展開となり他と変わらなくなります（コモディティ化を招く）。そうなると立地、価格、サービス、店舗規模など他店との消耗戦になっていくわけです。より良い立地。より安い価格。より手厚いサービス。大きな店舗を作って充実の品揃え。そういう競争です。

Amazonではあまり売上がない膨大な商品に目を付けました。この商品層をロングテール（長い尻尾）と呼びます。年に１個しか売れない商品でも売り上げになる。そのような商品は実店舗に置くことはできませんが、物理的な制限がないインターネット上のサイトでは可能です。もちろん強大な物流インフラを持っているから可能なことですが。少ない売上でも扱う商品数をけた外れに多くすることで全体の売上を積み重ねていく。そのようなロングテール戦略をとったのでした。

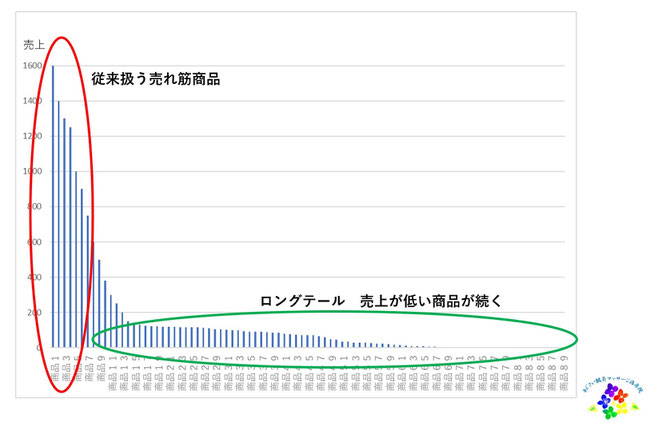
ロングテール部分を積分するとその面積はとてつもない広さになります。それは売れ筋の少ない品種でできる面積を超える程の。ロングテール戦略を知ったときに積分が頭に思い浮かべました。

私の仕事でいえば、毎年チェックしている国家試験の動向もそうです。あん摩マッサージ指圧師、はり師、きゅう師、柔道整復師の国家試験。それをグラフ化して動向を確認します。他にも理学療法士の動向も。経年の人数変化から業界の勢いや動向を視覚化します（微分）。これまでの合格者数の積み重ねから規模を比較します（積分）。

微分積分を知っていることで物事の見え方が増えるのではないしょうか。

甲野　功

電話　　　：070-6529-3668

メール　　：kouno.teate@gmail.com

ＬＩＮＥ　：@qee9465q

ご連絡お待ちしております。

院長の書いたコラムブログはこちら→詳しくはこちらへ